1. Въведение
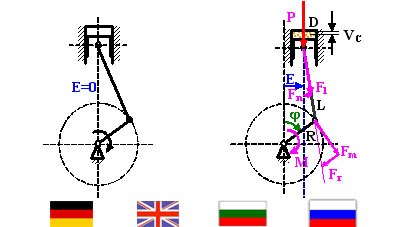
В класическата схема, по която са построени двигателите с вътрешно горене (ДВГ), оста на цилиндъра и оста на коляновия вал лежат в една равнина и са перпендикулярни една на друга. Тук ще покажа резултатите от теоретичното изследване на основни параметри на ДВГ, чиито оси на цилиндъра и на коляновия вал не лежат в една равнина, като оста на цилиндъра е успоредно отместена на разстояние E от традиционното си положение в равнината на въртене на коляното на коляновия вал, т.е. те са кръстосани (фигурата над заглавието). Разстоянието E ще наричаме ексцентрицитет.
Изследваните параметри като функция на ексцентрицитета са от две групи: енергетични – индикаторната работа (корелираща с индикаторната мощност) и средния въртящ момент; и силови – силите, приложени върху коляно-мотовилковия механизъм (КММ) и бутало-цилиндровата група (БЦГ). Заедно със средния въртящ момент ще изчисляваме и неговото средно квадратично отклонение (СКО) σ, даващо представа за равномерността на въртене на коляновия вал.
Индикаторната работа е
където Pv е налягането в цилиндъра като функция от обема на цилиндъра V.
Средният въртящ момент е
където Mφ е текущото значение на момента като функция от ъгъла φ, а n = 2 или 4 (за дву- или четири-тактов ДВГ).
Силите, приложени върху КММ и БЦГ, се изразяват чрез тригонометрични уравнения, а тяхната средна стойност се определя чрез решаване на определени интеграли, подобни на (2). При изследване размерите на ДВГ като функция от ексцентрицитета се вижда, че максималния обем на цилиндъра (Vmax) в двата края на дефиниционната област нараства до стойност, която расте с увеличаването дължината на мотовилката:
(3),
където VC е обема на горивната камера, S е хода на буталото, D е диаметъра на цилиндъра, L е дължината на мотовилката, R е дължината на коляното, E е ексцентрицитета на оста на цилиндъра. Дефиниционната област на размерите на такъв ДВГ е
L>R и |E|<L-R (4).
2. Математически модел за изследване параметрите в реален ДВГ посредством обработката на индикаторната му диаграма
Тук е показан вида на индикаторна диаграма на 2-тактов ДВГ. Процесите свиване (1-2) и разширяване (3-4) са политропни и за тях PVn=const. Процесът продухване (4-1) с определена точност също може да се представи с два политропни процеса. Процесът горене (2-3) е също политропен, но със силно променящ се показател n. Подобно е описанието на индикаторната диаграма и на 4-тактовия ДВГ. Интегралните уравнения (1) и (2) за процесите 3-4-1-2 нямат решение в елементарни функции, а за пресмятането на процеса горене (2-3) се предлагат различни математически модели. Това налага използването на цялостен математически модел за изчисляване на уравненията (1) и (2). Реализираният тук математически модел за изчисляване на налягането в цилиндъра при различни стойности на ексцентрицитета Е, се основава на получена реална индикаторна диаграма за съществуващ ДВГ, изпълнен по класическата схема (Е=0) при определен режим – подавано количество гориво и приложен товар. И като функция от отместването се определят изследваните енергетични характеристики и сили при запазване обема на цилиндъра постоянен (при запазване постоянна действителната степен на сгъстяване ε) и подаденото гориво. Индикаторните диаграми, служещи за основа на модела, са заснети посредством системата MIP (Combustion Analyzer), използвана в Българския морски флот.
3. Функционални зависимости на основните характеристики от ексцентрицитета
За няколко ДВГ са показани получените чрез математическия модел диаграми на интересуващите ни функционални зависимости като функция на нормирания ексцентрицитет e=E/R: индикаторната работа Aind, средния въртящ момент Mav, средното квадратично отклонение на въртящия момент σ и средните стойности на силите, приложени върху: буталния болт Fb, мотовилката и мотовилковия лагер Fl, двойката бутало-цилиндър Fn, перпендикулярно на коляното в мотовилковия лагер Fm, коляното и основния лагер Fr. Всички диаграми са построени с нормираните им стойности (в %), т.е. разделени на стойностите им при нулев ексцентрицитет (Е=0); диаграмите с индекс а са в характерни места по абсцисата с увеличен мащаб и намалена стъпка; силата Fn е показана чрез абсолютната си стойност |Fn| и чрез нейните съставляващи – положителната +Fn и абсолютната стойност на отрицателната |-Fn|.
3.1. ДВГ 6ДКРН 67/170-4, главен двигател на моторен кораб Станко Стайков (ДВГ прототип B&W K67GF) – дизелов, 2-тактов
Фиг. 3.1.1. Диаграма на нормираните зависимости на индикаторната работа Aind, средния въртящ момент Mav и СКО на момента σ
Фиг. 3.1.1.а. Диаграма на нормираните зависи мо сти на индикаторната работа Aind, средния въртящ момент Mav и СКО на момента σ - с намалена стъп ка по ексцентрицитета и увеличен мащаб по ординатата
Фиг. 3.1.2. Диаграма на нормираните зависимости на силите: Fr, Fl и Fm – средни стойности
Фиг. 3.1.3. Диаграма на нормираните зависимости на силата |Fn| и нейните съставляващи +Fn и |-Fn| – средни стойности
Фиг. 3.1.3.а. Диаграма на нормираните зависимо сти на силата |Fn| и нейните съставляващи +Fn и |-Fn| – средни стойности - с намалена стъпка по ексцентрицитета и увеличен мащаб по ординатата
3.2. ДВГ MAN-B&W 4S26MC, главен двигател на моторен кораб Полукс – дизелов, 2-тактов
Фиг. 3.2.1. Диаграма на нормираните зависимости на индикаторната работа Aind, средния въртящ момент Mav и СКО на момента σ
Фиг. 3.2.1.а. Диаграма на нормираните зависи мо сти на индикаторната работа Aind, средния въртящ момент Mav и СКО на момента σ - с намалена стъп ка по ексцентрицитета и увеличен мащаб по ординатата
Фиг. 3.2.2. Диаграма на нормираните зависимости на силите: Fr, Fl и Fm – средни стойности
Фиг. 3.2.3. Диаграма на нормираните зависимости на силата |Fn| и нейните съставляващи +Fn и |-Fn| – средни стойности
Фиг. 3.2.3.а. Диаграма на нормираните зависимо сти на силата |Fn| и нейните съставляващи +Fn и |-Fn| – средни стойности - с намалена стъпка по ексцентрицитета и увеличен мащаб по ординатата
3.3. ДВГ SULZER 5AL25/30, дизел-генератор № 1 на моторен кораб Рожен – дизелов, 4-тактов
Фиг. 3.3.1. Диаграма на нормираните зависимости на индикаторната работа Aind, средния въртящ момент Mav и СКО на момента σ
Фиг. 3.3.1.а. Диаграма на нормираните зависи мо сти на индикаторната работа Aind, средния въртящ момент Mav и СКО на момента σ - с намалена стъп ка по ексцентрицитета и увеличен мащаб по ординатата
Фиг. 3.3.2. Диаграма на нормираните зависимости на силите: Fr, Fl и Fm – средни стойности
Фиг. 3.3.3. Диаграма на нормираните зависимости на силата |Fn| и нейните съставляващи +Fn и |-Fn| – средни стойности
Фиг. 3.3.3.а. Диаграма на нормираните зависимо сти на силата |Fn| и нейните съставляващи +Fn и |-Fn| – средни стойности - с намалена стъпка по ексцентрицитета и увеличен мащаб по ординатата
3.4. ДВГ SULZER 8BAH22, дизел-генератор № 3 на моторен кораб Белмекен – дизелов, 4-тактов
Фиг. 3.4.1. Диаграма на нормираните зависимости на индикаторната работа Aind, средния въртящ момент Mav и СКО на момента σ
Фиг. 3.4.1.а. Диаграма на нормираните зависимости на индикаторната работа Aind, средния въртящ момент Mav и СКО на момента σ - с намалена стъпка по ексцентрицитета и увеличен мащаб по ординатата
Фиг. 3.4.2. Диаграма на нормираните зависимости на силите: Fr, Fl и Fm – средни стойности
Фиг. 3.4.3. Диаграма на нормираните зависимости на силата |Fn| и нейните съставляващи +Fn и |-Fn| – средни стойности
Фиг. 3.4.3.а. Диаграма на нормираните зависимости на силата |Fn| и нейните съставляващи +Fn и |-Fn| – средни стойности - с намалена стъпка по ексцентрицитета и увеличен мащаб по ординатата
4. Анализ на получените зависимости на характеристиките от отместванетоАнализът на функционалните зависимости на енергетичните характеристики и действащите сили показва следното:
4.1. При двутактовите ДВГ с увеличаване на отместването в положителна посока работата се увеличава, в отрицателна намалява; при еmax работата се увеличава до 108% – 125%, при е ≈ 1 работата се увеличава до 120%. При четиритактовите ДВГ графика на работата има характер на парабола, обърната надолу, т.е. работата намалява, като в отрицателна посока отначало се задържа много близо до 100%, но след това по-бързо слиза до по-ниски стойности; при еmax работата може да падне до 70% – 85%.
4.2. Функцията на средния въртящ момент представлява начупена линия, колебаеща се около линия, следваща изменението на работата. При двутактовите ДВГ при еmax средния въртящ момент стига до 105% - 130%, максимумите при e ≈ 1 имат стойности в интервала 105% - 125%. При четиритактовите ДВГ има само отделни пикове надминаващи 100%, но те са в границита на 101% - 102%.
4.3. Функцията на СКО на момента има характер на парабола, обърната с отвора надолу. Т.е. при увеличаване на отместването се увеличава равномерността на въртене на коляновия вал. При двутактовите ДВГ при отместване, близко до максималното, СКО намалява с 15% до 30%, при стойности на отместването e ≈ 1 СКО намалява с 3% до 10%. При четиритактовите ДВГ максимума на параболата е при e = [-0.9,-1.4] и има стойности около 101% - 102%, т.е. равномерността на въртене се влошава; при по-големи отмествания в отрицателна посока СКО пада бързо, но до по-високи стойности от стойностите при отместване в положителна посока.
4.4. Функционалните зависимостите на средните стойности на силите Fr и Fl се отклоняват незначително от 100%. При двутактовите ДВГ отклонението е в посока намаляване на средните им стойности; при четиритактовите двигатели силата Fr също намалява, но силата Fl се увеличава. Fm следва изменението на средния въртящ момент.
4.5. Силата |Fn| има характер на парабола с минимум 80% - 95% в интервала e = [0.1,0.4]. При максимално допустимите стойности на отместването, увеличението на тази сила може да стигне до 15 – 20 пъти. При отместване около e ≈ 1, увеличаването на средната стойност е в рамките от 5 до 15 пъти. При отместване по-голямо от 0.6 – 0.7, само едната съставляваща на тази сила е различна от нула; т.е. натоварена е само едната страна на двойката цилиндър/бутало.
5. Заключение
При положително отместване в двутактовите ДВГ може да се получи увеличаване на индикаторнате работа, т.е. на мощността на двигателя, и съществено на средния въртящ момент при забележимо увеличаване равномерността на въртене на коляновия вал. Всичко това се осъществява без изменение на количеството изгаряно гориво. Това води до увеличение на КПД на двигателя и намаляване ефективния разход на гориво. Т.е. ще се подобрят икономическите показатели на ДВГ, а от там и на цялата задвижвана от него система. При четиритактовите ДВГ увеличаване на индикаторната работа не може да се постигне, но е възможно неголямо увеличаване на въртящия момент.
Едновременно с това може да се постигне намаляване на загубите от триене в двойката бутало/цилиндър и тяхното износване, когато отместването е в зоната на минимума на силата |Fn|. Конструиране на двигател с отместване, водещо до съществено увеличаване на силата Fn, с цел да постигнем по-голямо увеличаване на работата и момента е оправдано, когато загубите от триенето се преодоляват чрез допълнителни конструктивни и технологични мерки. Една такава известна мярка е кръстоглавия двигател.
—————————————————————————————————
Публикувано в сп. "Машиностроене и електротехника" № 5/2005 год. на Научно-техническия съюз по машиностроене, България. Изнесен доклад на XII международна научно-техническа конференция "Транс & Мотауто '05" 2005 год. в гр. Велико Търново.
Няма коментари:
Публикуване на коментар